MPI Reduce and Allreduce
Author: Wes KendallIn the previous lesson, we went over an application example of using MPI_Scatter and MPI_Gather to perform parallel rank computation with MPI. We are going to expand on collective communication routines even more in this lesson by going over MPI_Reduce and MPI_Allreduce.
Note - All of the code for this site is on GitHub. This tutorial’s code is under tutorials/mpi-reduce-and-allreduce/code.
An introduction to reduce
Reduce is a classic concept from functional programming. Data reduction involves reducing a set of numbers into a smaller set of numbers via a function. For example, let’s say we have a list of numbers [1, 2, 3, 4, 5]. Reducing this list of numbers with the sum function would produce sum([1, 2, 3, 4, 5]) = 15. Similarly, the multiplication reduction would yield multiply([1, 2, 3, 4, 5]) = 120.
As you might have imagined, it can be very cumbersome to apply reduction functions across a set of distributed numbers. Along with that, it is difficult to efficiently program non-commutative reductions, i.e. reductions that must occur in a set order. Luckily, MPI has a handy function called MPI_Reduce that will handle almost all of the common reductions that a programmer needs to do in a parallel application.
MPI_Reduce
Similar to MPI_Gather, MPI_Reduce takes an array of input elements on each process and returns an array of output elements to the root process. The output elements contain the reduced result. The prototype for MPI_Reduce looks like this:
MPI_Reduce(
void* send_data,
void* recv_data,
int count,
MPI_Datatype datatype,
MPI_Op op,
int root,
MPI_Comm communicator)
The send_data parameter is an array of elements of type datatype that each process wants to reduce. The recv_data is only relevant on the process with a rank of root. The recv_data array contains the reduced result and has a size of sizeof(datatype) * count. The op parameter is the operation that you wish to apply to your data. MPI contains a set of common reduction operations that can be used. Although custom reduction operations can be defined, it is beyond the scope of this lesson. The reduction operations defined by MPI include:
MPI_MAX- Returns the maximum element.MPI_MIN- Returns the minimum element.MPI_SUM- Sums the elements.MPI_PROD- Multiplies all elements.MPI_LAND- Performs a logical and across the elements.MPI_LOR- Performs a logical or across the elements.MPI_BAND- Performs a bitwise and across the bits of the elements.MPI_BOR- Performs a bitwise or across the bits of the elements.MPI_MAXLOC- Returns the maximum value and the rank of the process that owns it.MPI_MINLOC- Returns the minimum value and the rank of the process that owns it.
Below is an illustration of the communication pattern of MPI_Reduce.
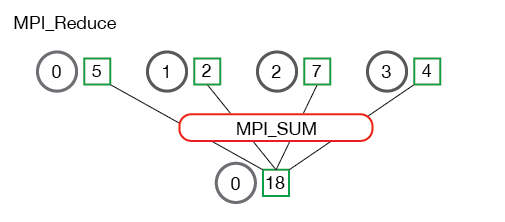
In the above, each process contains one integer. MPI_Reduce is called with a root process of 0 and using MPI_SUM as the reduction operation. The four numbers are summed to the result and stored on the root process.
It is also useful to see what happens when processes contain multiple elements. The illustration below shows reduction of multiple numbers per process.
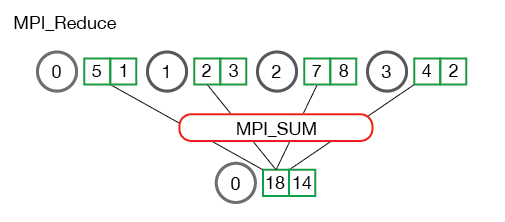
The processes from the above illustration each have two elements. The resulting summation happens on a per-element basis. In other words, instead of summing all of the elements from all the arrays into one element, the ith element from each array are summed into the ith element in result array of process 0.
Now that you understand how MPI_Reduce looks, we can jump into some code examples.
Computing average of numbers with MPI_Reduce
In the previous lesson, I showed you how to compute average using MPI_Scatter and MPI_Gather. Using MPI_Reduce simplifies the code from the last lesson quite a bit. Below is an excerpt from reduce_avg.c in the example code from this lesson.
float *rand_nums = NULL;
rand_nums = create_rand_nums(num_elements_per_proc);
// Sum the numbers locally
float local_sum = 0;
int i;
for (i = 0; i < num_elements_per_proc; i++) {
local_sum += rand_nums[i];
}
// Print the random numbers on each process
printf("Local sum for process %d - %f, avg = %f\n",
world_rank, local_sum, local_sum / num_elements_per_proc);
// Reduce all of the local sums into the global sum
float global_sum;
MPI_Reduce(&local_sum, &global_sum, 1, MPI_FLOAT, MPI_SUM, 0,
MPI_COMM_WORLD);
// Print the result
if (world_rank == 0) {
printf("Total sum = %f, avg = %f\n", global_sum,
global_sum / (world_size * num_elements_per_proc));
}
In the code above, each process creates random numbers and makes a local_sum calculation. The local_sum is then reduced to the root process using MPI_SUM. The global average is then global_sum / (world_size * num_elements_per_proc). If you run the reduce_avg program from the tutorials directory of the repo, the output should look similar to this.
>>> cd tutorials
>>> ./run.py reduce_avg
mpirun -n 4 ./reduce_avg 100
Local sum for process 0 - 51.385098, avg = 0.513851
Local sum for process 1 - 51.842468, avg = 0.518425
Local sum for process 2 - 49.684948, avg = 0.496849
Local sum for process 3 - 47.527420, avg = 0.475274
Total sum = 200.439941, avg = 0.501100
Now it is time to move on to the sibling of MPI_Reduce - MPI_Allreduce.
MPI_Allreduce
Many parallel applications will require accessing the reduced results across all processes rather than the root process. In a similar complementary style of MPI_Allgather to MPI_Gather, MPI_Allreduce will reduce the values and distribute the results to all processes. The function prototype is the following:
MPI_Allreduce(
void* send_data,
void* recv_data,
int count,
MPI_Datatype datatype,
MPI_Op op,
MPI_Comm communicator)
As you might have noticed, MPI_Allreduce is identical to MPI_Reduce with the exception that it does not need a root process id (since the results are distributed to all processes). The following illustrates the communication pattern of MPI_Allreduce:
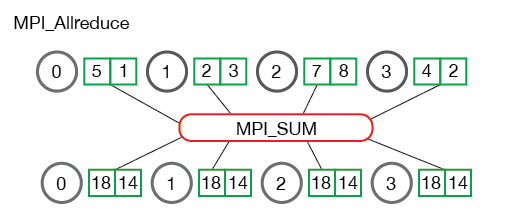
MPI_Allreduce is the equivalent of doing MPI_Reduce followed by an MPI_Bcast. Pretty simple, right?
Computing standard deviation with MPI_Allreduce
Many computational problems require doing multiple reductions to solve problems. One such problem is finding the standard deviation of a distributed set of numbers. For those that may have forgotten, standard deviation is a measure of the dispersion of numbers from their mean. A lower standard deviation means that the numbers are closer together and vice versa for higher standard deviations.
To find the standard deviation, one must first compute the average of all numbers. After the average is computed, the sums of the squared difference from the mean are computed. The square root of the average of the sums is the final result. Given the problem description, we know there will be at least two sums of all the numbers, translating into two reductions. An excerpt from reduce_stddev.c in the lesson code shows what this looks like in MPI.
rand_nums = create_rand_nums(num_elements_per_proc);
// Sum the numbers locally
float local_sum = 0;
int i;
for (i = 0; i < num_elements_per_proc; i++) {
local_sum += rand_nums[i];
}
// Reduce all of the local sums into the global sum in order to
// calculate the mean
float global_sum;
MPI_Allreduce(&local_sum, &global_sum, 1, MPI_FLOAT, MPI_SUM,
MPI_COMM_WORLD);
float mean = global_sum / (num_elements_per_proc * world_size);
// Compute the local sum of the squared differences from the mean
float local_sq_diff = 0;
for (i = 0; i < num_elements_per_proc; i++) {
local_sq_diff += (rand_nums[i] - mean) * (rand_nums[i] - mean);
}
// Reduce the global sum of the squared differences to the root
// process and print off the answer
float global_sq_diff;
MPI_Reduce(&local_sq_diff, &global_sq_diff, 1, MPI_FLOAT, MPI_SUM, 0,
MPI_COMM_WORLD);
// The standard deviation is the square root of the mean of the
// squared differences.
if (world_rank == 0) {
float stddev = sqrt(global_sq_diff /
(num_elements_per_proc * world_size));
printf("Mean - %f, Standard deviation = %f\n", mean, stddev);
}
In the above code, each process computes the local_sum of elements and sums them using MPI_Allreduce. After the global sum is available on all processes, the mean is computed so that local_sq_diff can be computed. Once all of the local squared differences are computed, global_sq_diff is found by using MPI_Reduce. The root process can then compute the standard deviation by taking the square root of the mean of the global squared differences.
Running the example code with the run script produces output that looks like the following:
>>> ./run.py reduce_stddev
mpirun -n 4 ./reduce_stddev 100
Mean - 0.501100, Standard deviation = 0.301126
Up next
Now that you are comfortable using all of the common collectives - MPI_Bcast, MPI_Scatter, MPI_Gather, and MPI_Reduce, we can utilize them to build a sophisticated parallel application. In the next lesson, we will start diving into MPI groups and communicators.
For all lessons, go the the MPI tutorials section.